Note
This paper is written in three main sections. In the first and third, Warren Weaver is responsible both for the ideas and the form. The middle section, namely 2) Communication Problems of Level A is an interpretation of mathematical papers by Dr. Claude E. Shannon of the Bell Telephone Laboratories. Dr. Shannon's work roots back, as von Neumann has pointed out, to Boltzmann's observation, in some of his work on statistical physics (1894), that entropy is related to "missing information," inasmuch as it is related to the number of alternatives which remain possible to a physical system after all the macroscopically observable information concerning it has been recorded. L. Szilard (Zsch. f. Phys. Vol. 53, 1925) extended this idea to a general discussion of information in physics, and von Neumann (Math. Foundation of Quantum Mechanics, Berlin, 1932, Chap. V) treated information in quantum mechanics and particle physics. Dr. Shannon's work connects more directly with certain ideas developed some twenty years ago by H. Nyquist and R. V. L. Hartley, both of the Bell Laboratories; and Dr. Shannon has himself emphasized that communication theory owes a great debt to Professor Norbert Wiener for much of its basic philosophy. Professor Wiener, on the other hand, points out that Shannon's early work on switching and mathematical logic antedated his own interest in this field; and generously adds that Shannon certainly deserves credit for independent development of such fundamental aspects of the theory as the introduction of entropic ideas. Shannon has naturally been specially concerned to push the applications to engineering communication, while Wiener has been more concerned with biological application (central nervous system phenomena, etc.).
1. Introductory Note on the General Setting of the Analytical Communication Studies
1.1. Communication
The word communication will be used here in a very broad sense to
include all of the procedures by which one mind may affect another. This,
of course, involves not only written and oral speech, but also music, the
pictorial arts, the theatre, the ballet, and in fact all human behavior.
In some connections it may be desirable to use a still broader definition
of communication, namely, one which would include the procedures by means
of which one mechanism (say automatic equipment to track an airplane and
to compute its probable future positions) affects another mechanism (say
a guided missile chasing this airplane).
The language of this memorandum will often appear to refer to the special,
but still very broad and important, field of the communication of speech;
but practically everything said applies equally well to music of any sort,
and to still or moving pictures, as in television.
1.2. Three Levels of Communications Problems
Relative to the broad subject of communication, there seem to be problems at three levels. Thus it seems reasonable to ask, serially:
LEVEL A. How accurately can the symbols of communication be transmitted? (The technical problem.)
LEVEL B. How precisely do the transmitted symbols convey the desired meaning? (The semantic problem.)
LEVEL C. How effectively does the received meaning affect conduct in the desired way? (The effectiveness problem.)
The technical problems are concerned with the accuracy of transference from sender to receiver of sets of symbols (written speech), or of a continuously varying signal (telephonic or radio transmission of voice or music), or of a continuously varying two-dimensional pattern (television), etc. Mathematically, the first involves transmission of a finite set of discrete symbols, the second the transmission of one continuous function of time, and the third the transmission of many continuous functions of time or of one continuous function of time and of two space coordinates.
The semantic problems are concerned with the identity, or satisfactorily
close approximation, in the interpretation of meaning by the receiver, as
compared with the intended meaning of the sender. This is a very deep and
involved situation, even when one deals only with the relatively simpler
problems of communicating through speech. One essential complication is illustrated
by the remark that if Mr. X is suspected not to understand what Mr. Y says,
then it is theoretically not possible, by having Mr. Y do nothing but talk
further with Mr. X, completely to clarify this situation in any finite time.
If Mr. Y says "Do you now understand me?" and Mr. X says "Certainly,
I do;" this is not necessarily a certification that understanding has
been achieved. It may just be that Mr. X did not understand the question.
If this sounds silly, try it again as "Czy pan mnie rozumie?" with
the answer "Hai wakkate imasu." I think that this basic difficulty
(1) is, at least in the restricted field of speech communication, reduced
to a tolerable size (but never completely eliminated) by "explanations" which
(a) are presumably never more than approximations to the ideas being explained,
but which (b) are understandable since they are phrased in language which
has previously been made reasonably clear by operational means. For example,
it does not take long to make the symbol for "yes" in any language
operationally understandable.
The semantic problem has wide ramifications if one thinks of communication
in general. Consider, for example, the meaning to a Russian of a U.S. newsreel
picture.
The effectiveness problems are concerned with the success with
which the meaning conveyed to the receiver leads to the desired conduct on
his part. It may seem at first glance undesirably narrow to imply that the
purpose of all communication is to influence the conduct of the receiver.
But with any reasonably broad definition of conduct, it is clear that communication
either affects conduct or is without any discernible and probable effect
at all.
The problem of effectiveness involves aesthetic considerations in the case
of the fine arts. In the case of speech, written or oral, it involves considerations
which range all the way from the mere mechanics of style, through all the
psychological and emotional aspects of propaganda theory, to those value
judgments which are necessary to give useful meaning to the words "success" and "desired" in
the opening sentence of this section on effectiveness.
The effectiveness problem is closely interrelated with the semantic problem,
and overlaps it in a rather vague way; and there is in fact overlap between
all of the suggested categories of problems.
1.3. Comments
So stated, one would be inclined to think that Level A is a relatively superficial one, involving only the engineering details of good design of a communication system; while Band C seem to contain most if not all of the philosophical content of the general problem of communication.
The mathematical theory of the engineering aspects of communication, as developed chiefly by Claude Shannon at the Bell Telephone Laboratories, admittedly applies in the first instance only to problem A, namely, the technical problem of accuracy of transference of various types of signals from sender to receiver. But the theory has, I think, a deep significance which proves that the preceding paragraph is seriously inaccurate. Part of the significance of the new theory comes from the fact that levels B and C, above, can make use only of those signal accuracies which turn out to be possible when analyzed at Level A. Thus any limitations discovered in the theory at Level A necessarily apply to levels B and C. But a larger part of the significance comes from the fact that the analysis at Level A discloses that this level overlaps the other levels more than one could possible naively suspect. Thus the theory of Level A is, at least to a significant degree, also a theory of levels B and C. I hope that the succeeding parts of this memorandum will illuminate and justify these last remarks.
2. Communication Problems at Level A
2.1. A Communication System and Its Problems
The communication system considered may be symbolically represented as follows:
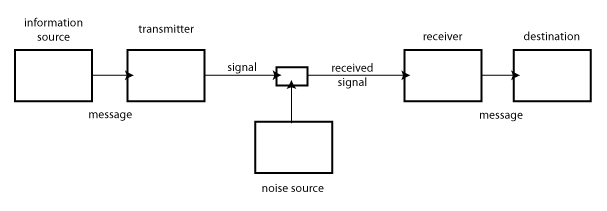
The information source selects a desired message out of a set of possible messages (this is a particularly important remark, which requires considerable explanation later). The selected message may consist of written or spoken words, or of pictures, music, etc.
The transmitter changes this message into the signal which is actually sent over the communication channel from the transmitter to the receiver. In the case of telephony, the channel is a wire, the signal a varying electrical current on this wire; the transmitter is the set of devices (telephone transmitter, etc.) which change the sound pressure of the voice into the varying electrical current. In telegraphy, the transmitter codes written words into sequences of interrupted currents of varying lengths (dots, dashes, spaces). In oral speech, the information source is the brain, the transmitter is the voice mechanism producing the varying sound pressure (the signal) which is transmitted through the air (the channel). In radio, the channel is simply space (or the aether, if anyone still prefers that antiquated and misleading word), and the signal is the electromagnetic wave which is transmitted.
The receiver is a sort of inverse transmitter, changing the transmitted signal back into a message, and handing this message on to the destination. When I talk to you, my brain is the information source, yours the destination; my vocal system is the transmitter, and your ear and the associated eighth nerve is the receiver.
In the process of being transmitted, it is unfortunately characteristic that certain things are added to the signal which were not intended by the information source. These unwanted additions may be distortions of sound (in telephony, for example) or static (in radio), or distortions in shape or shading of picture (television), or errors in transmission (telegraphy or facsimile), etc. All of these changes in the transmitted signal are called noise.
The kind of questions which one seeks to ask concerning such a communication system are:
a. How does one measure amount of information?
b. How does one measure the capacity of a communication channel?
c. The action of the transmitter in changing the message into the signal often involves a coding process. What are the characteristics of an efficient coding process? And when the coding is as efficient as possible, at what rate can the channel convey information?
d. What are the general characteristics of noise? How does noise affect the accuracy of the message finally received at the destination? How can one minimize the undesirable effects of noise, and to what extent can they be eliminated?
e. If the signal being transmitted is continuous (as in oral speech or music) rather than being formed of discrete symbols (as in written speech, telegraphy, etc.), how does this fact affect the problem?
We will now state, without any proofs and with a minimum of mathematical terminology, the main results which Shannon has obtained.
2.2. Information
The word information, in this theory, is used in a special sense that must not be confused with its ordinary usage. In particular, information must not be confused with meaning.
In fact, two messages, one of which is heavily loaded with meaning and the other of which is pure nonsense, can be exactly equivalent, from the present viewpoint, as regards information. It is this, undoubtedly, that Shannon means when he says that "the semantic aspects of communication are irrelevant to the engineering aspects." But this does not mean that the engineering aspects are necessarily irrelevant to the semantic aspects.
To be sure, this word information in communication theory relates not so
much to what you do say, as to what you could say.
That is, information is a measure of one's freedom of choice when one selects
a message. If one is confronted with a very elementary situation where he
has to choose one of two alternative messages, then it is arbitrarily said
that the information, associated with this situation, is unity. Note that
it is misleading (although often convenient) to say that one or the other
message conveys unit information. The concept of information applies not
to the individual messages (as the concept of meaning would), but rather
to the situation as a whole, the unit information indicating that in this
situation one has an amount of freedom of choice, in selecting a message,
which it is convenient to regard as a standard or unit amount.
The two messages between which one must choose, in such a selection, can be anything one likes. One might be the text of the King James Version of the Bible, and the other might be "Yes." The transmitter might code these two messages so that "zero" is the signal for the first, and "one" the signal for the second; or so that a closed circuit (current flowing) is the signal for the first, and an open circuit (no current flowing) the signal for the second. Thus the two positions, closed and open, of a simple relay, might correspond to the two messages.
To be somewhat more definite, the amount of information is defined, in the simplest cases, to be measured by the logarithm of the number of available choices. It being convenient to use logarithms (2) to the base 2, rather than common or Briggs' logarithm to the base 10, the information, when there are only two choices, is proportional to the logarithm of 2 to the base 2. But this is unity; so that a two-choice situation is characterized by information of unity, as has already been stated above. This unit of information is called a "bit," this word, first suggested by John W. Tukey, being a condensation of "binary digit." When numbers are expressed in the binary system there are only two digits, namely 0 and 1; just as ten digits, 0 to 9 inclusive, are used in the decimal number system which employs 10 as a base. Zero and one may be taken symbolically to represent any two choices, as noted above; so that "binary digit" or "bit" is natural to associate with the two-choice situation which has unit information.
If one has available say 16 alternative messages among which he is equally
free to choose, then since 16 = 24 so that log2 16 = 4, one says that this
situation is characterized by 4 bits of information.
It doubtless seems queer, when one first meets it, that information is defined
as the logarithm of the number of choices. But in the unfolding of the theory,
it becomes more and more obvious that logarithmic measures are in fact the
natural ones. At the moment, only one indication of this will be given. It
was mentioned above that one simple on-or-off relay, with its two positions
labeled, say, 0 and 1 respectively, can handle a unit information situation,
in which there are but two message choices. If one relay can handle unit
information, how much can be handled by say three relays? It seems very reasonable
to want to say that three relays could handle three times as much information
as one. And this indeed is the way it works out if one uses the logarithmic
definition of information. For three relays are capable of responding to
23 or 8 choices, which symbolically might be written as 000, 001, 011, 010,
100, 110, 101, 111, in the first of which all three relays are open, and
in the last of which all three relays are closed. And the logarithm to the
base 2 of 23 is 3, so that the logarithmic measure assigns three units of
information to this situation, just as one would wish. Similarly, doubling
the available time squares the number of possible messages, and doubles the
logarithm; and hence doubles the information if it is measured logarithmically.
The remarks thus far relate to artificially simple situations where the information source is free to choose only between several definite messages - like a man picking out one of a set of standard birthday greeting telegrams. A more natural and more important situation is that in which the information source makes a sequence of choices from some set of elementary symbols, the selected sequence then forming the message. Thus a man may pick out one word after another, these individually selected words then adding up to form the message.
At this point an important consideration which has been in the background, so far, comes to the front for major attention. Namely, the role which probability plays in the generation of the message. For as the successive symbols are chosen, these choices are, at least from the point of view of the communication system, governed by probabilities; and in fact by probabilities which are not independent, but which, at any stage of the process, depend upon the preceding choices. Thus, if we are concerned with English speech, and if the last symbol chosen is "the," then the probability that the next word be an article, or a verb form other than a verbal, is very small. This probabilistic influence stretches over more than two words, in fact. After the three words "in the event" the probability for "that" as the next word is fairly high, and for "elephant" as the next word is very low.
That there are probabilities which exert a certain degree of control over the English language also becomes obvious if one thinks, for example, of the fact that in our language the dictionary contains no words whatsoever in which the initial letter j is followed by b, c, d, f, g, j, k, l, q, r, t, v, w, x, or z; so that the probability is actually zero that an initial j be followed by any of these letters. Similarly, anyone would agree that the probability is low for such a sequence of words as "Constantinople fishing nasty pink." Incidentally, it is low, but not zero; for it is perfectly possible to think of a passage in which one sentence closes with "Constantinople fishing," and the next begins with "Nasty pink." And we might observe in passing that the unlikely four-word sequence under discussion has occurred in a single good English sentence, namely the one above.
A system which produces a sequence of symbols (which may, of course, be letters or musical notes, say, rather than words) according to certain probabilities is called a stochastic process, and the special case of a stochastic process in which the probabilities depend on the previous events, is called a Markoff process or a Markoff chain. Of the Markoff processes which might conceivably generate messages, there is a special class which is of primary importance for communication theory, these being what are called ergodic processes. The analytical details here are complicated and the reasoning so deep and involved that it has taken some of the best efforts of the best mathematicians to create the associated theory; but the rough nature of an ergodic process is easy to understand. It is one which produces a sequence of symbols which would be a poll-taker's dream, because any reasonably large sample tends to be representative of the sequence as a whole. Suppose that two persons choose samples in different ways, and study what trends their statistical properties would show as the samples become larger. If the situation is ergodic, then those two persons, however they may have chosen their samples, agree in their estimates of the properties of the whole. Ergodic systems, in other words, exhibit a particularly safe and comforting sort of statistical regularity.
Now let us return to the idea of information. When we have an
information source which is producing a message by successively selecting
discrete symbols (letters, words, musical notes, spots of a certain size,
etc.), the probability of choice of the various symbols at one stage of the
process being dependent on the previous choices (i.e., a Markoff process),
what about the information associated with this procedure?
The quantity which uniquely meets the natural requirements that one sets
up for "information" turns out to be exactly that which is known
in thermodynamics as entropy. It is expressed in terms of the various
probabilities involved - those of getting to certain stages in the process
of forming messages, and the probabilities that, when in those stages, certain
symbols be chosen next. The formula, moreover, involves the logarithm of
probabilities, so that it is a natural generalization of the logarithmic
measure spoken of above in connection with simple cases.
To those who have studied the physical sciences, it is most significant that an entropy-like expression appears in the theory as a measure of information. Introduced by Clausius nearly one hundred years ago, closely associated with the name of Boltzmann, and given deep meaning by Gibbs in his classic work on statistical mechanics, entropy has become so basic and pervasive a concept that Eddington remarks "The law that entropy always increases - the second law of thermodynamics - holds, I think, the supreme position among the laws of Nature."
In the physical sciences, the entropy associated with a situation is a measure of the degree of randomness, or of "shuffledness" if you will, in the situation; and the tendency of physical systems to become less and less organized, to become more and more perfectly shuffled, is so basic that Eddington argues that it is primarily this tendency which gives time its arrow - which would reveal to us, for example, whether a movie of the physical world is being run forward or backward.
Thus when one meets the concept of entropy in communication theory, he has a right to be rather excited - a right to suspect that one has hold of something that may turn out to be basic and important. That information be measured by entropy is, after all, natural when we remember that information, in communication theory, is associated with the amount of freedom of choice we have in constructing messages. Thus for a communication source one can say, just as he would also say it of a thermodynamic ensemble, "This situation is highly organized, it is not characterized by a large degree of randomness or of choice - that is to say, the information (or the entropy) is low." We will return to this point later, for unless I am quite mistaken, it is an important aspect of the more general significance of this theory.
Having calculated the entropy (or the information, or the freedom of choice) of a certain information source, one can compare this to the maximum value this entropy could have, subject only to the condition that the source continue to employ the same symbols. The ratio of the actual to the maximum entropy is called the relative entropy of the source. If the relative entropy of a certain source is, say .8, this roughly means that this source is, in its choice of symbols to form a message, about 80 per cent as free as it could possibly be with these same symbols. One minus the relative entropy is called the redundancy. This is the fraction of the structure of the message which is determined not by the free choice of the sender, but rather by the accepted statistical rules governing the use of the symbols in question. It is sensibly called redundancy, for this fraction of the message is in fact redundant in something close to the ordinary sense; that is to say, this fraction of the message is unnecessary (and hence repetitive or redundant) in the sense that if it were missing the message would still be essentially complete, or at least could be completed.
It is most interesting to note that the redundancy of English is just about
50 per cent (3), so that about half of the letters or words we choose in
writing or speaking are under our free choice, and about half (although we
are not ordinarily aware of it) are really controlled by the statistical
structure of the language.
Apart from more serious implications, which again we will postpone to our
final discussion, it is interesting to note that a language must have at
least 50 per cent of real freedom (or relative entropy) in the choice of
letters if one is to be able to construct satisfactory crossword puzzles.
If it has complete freedom, then every array of letters is a crossword puzzle.
If it has only 20 per cent of freedom, then it would be impossible to construct
crossword puzzles in such complexity and number as would make the game popular.
Shannon has estimated that if the English language had only about 30 per
cent redundancy, then it would be possible to construct three-dimensional
crossword puzzles. .
Before closing this section on information, it should be noted that the real reason that Level A analysis deals with a concept of information which characterizes the whole statistical nature of the information source, and is not concerned with the individual messages (and not at all directly concerned with the meaning of the individual messages) is that from the point of view of engineering, a communication system must face the problem of handling any message that the source can produce. If it is not possible or practicable to design a system which can handle everything perfectly, then the system should be designed to handle well the jobs it is most likely to be asked to do, and should resign itself to be less efficient for the rare task. This sort of consideration leads at once to the necessity of characterizing the statistical nature of the whole ensemble of messages which a given kind of source can and will produce. And information, as used in communication theory, does just this.
Although it is not at all the purpose of this paper to be concerned with mathematical details, it nevertheless seems essential to have as good an understanding as possible of the entropy-like expression which measures information. If one is concerned, as in a simple case, with a set of n independent symbols, or a set of n independent complete messages for that matter, whose probabilities of choice are p1, p2 . . . p, then the actual expression for the information is
H = - [p1 log p1 + p2 log p2 + . . . + pn log pn],
or
H = - ∑ pi log pi.
Where (4) the symbol ∑ indicates, as is usual in mathematics, that one is to sum all terms like the typical one, pi log pi, written as a defining sample.
This looks a little complicated; but let us see how this expression behaves
in some simple cases. Suppose first that we are choosing only between two
possible messages, whose probabilities are then p1 for the first and
p2 = 1 – p1 for the other. If one reckons, for this case, the numerical value
of H, it turns out that H has its largest value, namely one, when the two
messages are equally probable; that is to say when p1 = p2 = 1/2; that is
to say, when one is completely free to choose between the two messages. Just
as soon as one message becomes more probable than the other (p1 greater than
p2, say), the value of H decreases. And when one message is very probable
(p1 almost one and p2 almost zero, say), the value of H is very small (almost
zero).
In the limiting case where one probability is unity (certainty) and all the
others zero (impossibility), then H is zero (no uncertainty at all - no freedom
of choice - no information).
Thus H is largest when the two probabilities are equal (i.e., when one is completely free and unbiased in the choice), and reduces to zero when one's freedom of choice is gone. The situation just described is in fact typical. If there are many, rather than two, choices, then H is largest when the probabilities of the various choices are as nearly equal as circumstances permit - when one has as much freedom as possible in making a choice, being as little as possible driven toward some certain choices which have more than their share of probability. Suppose, on the other hand, that one choice has a probability near one so that all the other choices have probabilities near zero. This is clearly a situation in which one is heavily influenced toward one particular choice, and hence has little freedom of choice. And H in such a case does calculate to have a very small value - the information (the freedom of choice, the uncertainty) is low.
When the number of cases is fixed, we have just seen that then the information is the greater, the more nearly equal are the probabilities of the various cases. There is another important way of increasing H, namely by increasing the number of cases. More accurately, if all choices are equally likely, the more choices there are, the larger H will be. There is more "information" if you select freely out of a set of fifty standard messages, than if you select freely out of a set of twenty-five.
2.3. Capacity of a Communication Channel
After the discussion of the preceding section, one is not surprised that the capacity of a channel is to be described not in terms of the number of symbols it can transmit, but rather in terms of the information it transmits. Or better, since this last phrase lend itself particularly well to a misinterpretation of the word information, the capacity of a channel is to be described in terms of its ability to transmit what is produced out of source of a given information.
If the source is of a simple sort in which all symbols are of the same time duration (which is the case, for example, with teletype), if the source is such that each symbol chosen represents s bits of information (being freely chosen from among 28 symbols) , and if the channel can transmit, say n symbols per second, then the capacity of C of the channel is defined to be ns bits per second.
In a more general case, one has to take account of the varying lengths of the various symbols. Thus the general expression for capacity of a channel involves the logarithm of the numbers of symbols of certain time duration (which introduces, of course, the idea of information and corresponds to the factor s in it simple case of the preceding paragraph); and also involves the number of such symbols handled (which corresponds to the factor n of the preceding paragraph). Thus in the general case, capacity measures not the number of symbols transmitted per second, but rather the amount of information transmitted per second, using bits per second as its unit.
2.4. Coding
At the outset it was pointed out that the transmitter accepts the message and turns it into something called the signal, the latter being what actually passes over the channel to the receiver.
The transmitter, in such a case as telephony, merely changes the audible voice signal over into something (the varying electrical current on the telephone wire) which is at once clearly different but clearly equivalent. But the transmitter may carry out a much more complex operation on the message to produce the signal. It could, for example, take a written message and use some code to encipher this message into, say a sequence of numbers; these numbers then being sent over the channel as the signal.
Thus one says, in general, that the function of the transmitter is to encode, and that of the receiver to decode, the message. The theory provides for very sophisticated transmitters and receivers - such, for example, as possess "memories," so that the way they encode a certain symbol of the message depends not only upon this one symbol, but also upon previous symbols of the message and the way they have been encoded.
We are now in a position to state the fundamental theorem, produced in this theory, for a noiseless channel transmitting discrete symbols. This theorem relates to a communication channel which has a capacity of C bits per second, accepting signals from a source of entropy (or information) of H bits per second. The theorem states that by devising proper coding procedures for the transmitter it is possible to transmit symbols over the channel at an average rate (5) which is nearly C/H, but which, no matter how clever the coding, can never be made to exceed C/H.
The significance of this theorem is to be discussed more usefully a little later, when we have the more general case when noise is present. For the moment, though, it is important to notice the critical role which coding plays.
Remember that the entropy (or information) associated with the process
which generates messages or signals is determined by the statistical character
of the process - by the various probabilities for arriving at message situations
and for choosing, when in those situations, the next symbols. The statistical
nature of messages is entirely determined by the character of the
source.
But the statistical character of the signal as actually transmitted by a
channel, and hence the entropy in the channel, is determined both by what
one attempts to feed into the channel and by the capabilities of the channel
to handle different signal situations. For example, in telegraphy, there
have to be spaces between dots and dots, between dots and dashes, and between
dashes and dashes, or the dots and dashes would not be recognizable.
Now it turns out that when a channel does have certain constraints of this sort, which limit complete signal freedom, there are certain statistical signal characteristics which lead to a signal entropy which is larger than it would be for any other statistical signal structure, and in this important case, the signal entropy is exactly equal to the channel capacity.
In terms of these ideas, it is now possible precisely to characterize the most efficient kind of coding. The best transmitter, in fact, is that which codes the message in such a way that the signal has just those optimum statistical characteristics which are best suited to the channel to be used - which in fact maximize the signal (or one may say, the channel) entropy and make it equal to the capacity C of the channel.
This kind of coding leads, by the fundamental theorem above, to the maximum rate C/H for the transmission of symbols. But for this gain in transmission rate, one pays a price. For rather perversely it happens that as one makes the coding more and more nearly ideal, one is forced to longer and longer delays in the process of coding. Part of this dilemma is met by the fact that in electronic equipment "long" may mean an exceedingly small fraction of a second, and part by the fact that one makes a compromise, balancing the gain in transmission rate against loss of coding time.
2.5. Noise
How does noise affect information? Information is, we must steadily remember, a measure of one's freedom of choice in selecting a message. The greater this freedom of choice, and hence the greater the information, the greater is the uncertainty that the message actually selected is some particular one. Thus greater freedom of choice, greater uncertainty, greater information go hand in hand.
If noise is introduced, then the received message contains certain distortions, certain errors, certain extraneous material, that would certainly lead one to say that the received message exhibits, because of the effects of the noise, an increased uncertainty. But if the uncertainty is increased, the information is increased, and this sounds as though the noise were beneficial !
It is generally true that when there is noise, the received signal exhibits
greater information - or better, the received signal is selected out of a
more varied set than is the transmitted signal. This is a situation which
beautifully illustrates the semantic trap into which one can fall if he does
not remember that "information" is used here with a special meaning
that measures freedom of choice and hence uncertainty as to what choice has
been made. It is therefore possible for the word information to have either
good or bad connotations. Uncertainty which arises by virtue of freedom of
choice on the part of the sender is desirable uncertainty. Uncertainty which
arises because of errors or because of the influence of noise is undesirable
uncertainty.
It is thus clear where the joker is in saying that the received signal has
more information. Some of this information is spurious and undesirable and
has been introduced via the noise. To get the useful information in the received
signal we must subtract out this spurious portion.
Before we can clear up this point we have to stop for a little detour. Suppose one has two sets of symbols, such as the message symbols generated by the information source, and the signal symbols which are actually received. The probabilities of these two sets of symbols are interrelated, for clearly the probability of receiving a certain symbol depends upon what symbol was sent. With no errors from noise or from other causes, the received signals would correspond precisely to the message symbols sent; and in the presence of possible error, the probabilities for received symbols would obviously be loaded heavily on those which correspond, or closely correspond, to the message symbols sent.
Now in such a situation one can calculate what is called the entropy of one set of symbols relative to the other. Let us, for example, consider the entropy of the message relative to the signal. It is unfortunate that we cannot understand the issues involved here without going into some detail. Suppose for the moment that one knows that a certain signal symbol has actually been received. Then each message symbol takes on a certain probability - relatively large for the symbol identical with or the symbols similar to the one received, and relatively small for all others. Using this set of probabilities, one calculates a tentative entropy value. This is the message entropy on the assumption of a definite known received or signal symbol. Under any good conditions its value is low, since the probabilities involved are not spread around rather evenly on the various cases, but are heavily loaded on one or a few cases. Its value would be zero in any case where noise was completely absent, for then, the signal symbol being known, all message probabilities would be zero except for one symbol (namely the one received), which would have a probability of unity.
For each assumption as to the signal symbol received, one can calculate one of these tentative message entropies. Calculate all of them, and then average them, weighting each one in accordance with the probability of the signal symbol assumed in calculating it. Entropies calculated in this way, when there are two sets of symbols to consider, are called relative entropies. The particular one just described is the entropy of the message relative to the signal, and Shannon has named this also the equivocation.
From the way this equivocation is calculated, we can see what its significance is. It measures the average uncertainty in the message when the signal is known. If there were no noise, then there would be no uncertainty concerning the message if the signal is known. If the information source has any residual uncertainty after the signal is known, then this must be undesirable uncertainty due to noise.
The discussion of the last few paragraphs centers around the quantity "the average uncertainty in the message source when the received signal is known." It can equally well be phrased in terms of the similar quantity "the average uncertainty concerning the received signal when the message sent is known." This latter uncertainty would, of course, also be zero if there were no noise. As to the interrelationship of these quantities, it is easy to prove that
H(x) - Hy(x) = H(y) - Hx(y)
where H(x) is the entropy or information of the source of messages; H(y) the
entropy or information of received signals; Hy(x) the equivocation,
or the uncertainty in the message source if the signal be known;
Hx(y) the
uncertainty in the received signals if the messages sent be known, or the
spurious part of the received signal information which is due to noise. The
right side of this equation is the useful information which is transmitted
in spite of the bad effect of the noise.
It is now possible to explain what one means by the capacity C of a noisy channel. It is, in fact, defined to be equal to the maximum rate (in bits per second) at which useful information (i.e., total uncertainty minus noise uncertainty) can be transmitted over the channel.
Why does one speak, here, of a "maximum" rate? What can one do, that is, to make this rate larger or smaller? The answer is that one can affect this rate by choosing a source whose statistical characteristics are suitably related to the restraints imposed by the nature of the channel. That is, one can maximize the rate of transmitting useful information by using proper coding.
And now, finally, let us consider the fundamental theorem for a noisy channel. Suppose that this noisy channel has, in the sense just described, a capacity C, suppose it is accepting from an information source characterized by an entropy of H(x) bits per second, the entropy of the received signals being H(y) bits per second. If the channel capacity C is equal to or larger than H(x), then by devising appropriate coding systems, the output of the source can be transmitted over the channel with as little error as one pleases. However small a frequency of error you specify, there is a code which meets the demand. But if the channel capacity C is less than H(x), the entropy of the source from which it accepts messages, then it is impossible to devise codes which reduce the error frequency as low as one may please.
However clever one is with the coding process, it will always be true that after the signal is received there remains some undesirable (noise) uncertainty about what the message was; and this undesirable uncertainty - this equivocation - will always be equal to or greater than H(x) - C. Furthermore, there is always at least one code which is capable of reducing this undesirable uncertainty, concerning the message, down to a value which exceeds H(x) - C by an arbitrarily small amount.
The most important aspect, of course, is that the minimum undesirable or spurious uncertainties cannot be reduced further, no matter how complicated or appropriate the coding process. This powerful theorem gives a precise and almost startlingly simple description of the utmost dependability one can ever obtain from a communication channel which operates in the presence of noise.
One practical consequence, pointed out by Shannon, should be noted. Since English is about 50 per cent redundant, it would be possible to save about one-half the time of ordinary telegraphy by a proper encoding process, provided one were going to transmit over a noiseless channel. When there is noise on a channel, however, there is some real advantage in not using a coding process that eliminates all of the redundancy. For the remaining redundancy helps combat the noise. This is very easy to see, for just because of the fact that the redundancy of English is high, one has, for example, little or no hesitation about correcting errors in spelling that have arisen during transmission.
2.6. Continuous Messages
Up to this point we have been concerned with messages formed out of discrete symbols, as words are formed of letters, sentences of words, a melody of notes, or a halftone picture of a finite number of discrete spots. What happens to the theory if one considers continuous messages, such as the speaking voice with its continuous variation of pitch and energy?
Very roughly one may say that the extended theory is somewhat more difficult and complicated mathematically, but not essentially different. Many of the above statements for the discrete case require no modification, and others require only minor change.
One circumstance which helps a good deal is the following. As a practical matter, one is always interested in a continuous signal which is built up of simple harmonic constituents of not all frequencies, but rather of frequencies which lie wholly within a band from zero frequency to, say, a frequency of W cycles per second. Thus although the human voice does contain higher frequencies, very satisfactory communication can be achieved over a telephone channel that handles frequencies only up to, say four thousand. With frequencies up to ten or twelve thousand, high fidelity radio transmission of symphonic music is possible, etc.
There is a very convenient mathematical theorem which states that a continuous signal, T seconds in duration and band-limited in frequency to the range from 0 to W, can be completely specified by stating 2TW numbers. This is really a remarkable theorem. Ordinarily a continuous curve can be only approximately characterized by stating any finite number of points through which it passes, and an infinite number would in general be required for complete information about the curve. But if the curve is built up out of simple harmonic constituents of a limited number of frequencies, as a complex sound is built up out of a limited number of pure tones, then a finite number of parameters is all that is necessary. This has the powerful advantage of reducing the character of the communication problem for continuous signals from a complicated situation where one would have to deal with an infinite number of variables to a considerably simpler situation where one deals with a finite (though large) number of variables.
In the theory for the continuous case there are developed formulas which describe the maximum capacity C of a channel of frequency bandwidth W, when the average power used in transmitting is P, the channel being subject to a noise of power N, this noise being "white thermal noise" of a special kind which Shannon defines. This white thermal noise is itself band limited in frequency, and the amplitudes of the various frequency constituents are subject to a normal (Gaussian) probability distribution. Under these circumstances, Shannon obtains the theorem, again really quite remarkable in its simplicity and its scope, that it is possible, by the best coding, to transmit binary digits at the rate of
W log2 P+N/N
bits per second and have an arbitrarily low frequency of error. But this rate cannot possibly be exceeded, no matter how clever the coding, without giving rise to a definite frequency of errors. For the case of arbitrary noise, rather than the special "white thermal" noise assumed above, Shannon does not succeed in deriving one explicit formula for channel capacity, but does obtain useful upper and lower limits for channel capacity. And he also derives limits for channel capacity when one specifies not the average power of the transmitter, but rather the peak instantaneous power.
Finally it should be stated that Shannon obtains results which are necessarily somewhat less specific, but which are of obviously deep and sweeping significance, which, for a general sort of continuous message or signal, characterize the fidelity of the received message, and the concepts of rate at which a source generates information, rate of transmission, and channel capacity, all of these being relative to certain fidelity requirements.
3. The Interrelationship of the Three Levels of Communication Problems
3.1. Introductory
In the first section of this paper it was suggested that there are three levels at which one may consider the general communication problem. Namely, one may ask:
LEVEL A. How accurately can the symbols of communication be transmitted?
LEVEL B. How precisely do the transmitted symbols convey the desired meaning?
LEVEL C. How effectively does the received meaning affect conduct in the desired way?
It was suggested that the mathematical theory of communication, as developed by Shannon, Wiener, and others, and particularly the more definitely engineering theory treated by Shannon, although ostensibly applicable only to Level A problems, actually is helpful and suggestive for the level B and C problems.
We then took a look, in section 2, at what this mathematical theory is, what concepts it develops, what results it has obtained. It is the purpose of this concluding section to review the situation, and see to what extent and in what terms the original section was justified in indicating that the progress made at Level A is capable of contributing to levels B and C, was justified in indicating that the interrelation of the three levels is so considerable that one's final conclusion may be that the separation into the three levels is really artificial and undesirable.
3.2. Generality of the Theory at level A
The obvious first remark, and indeed the remark that carries the major burden of the argument, is that the mathematical theory is exceedingly general in its scope, fundamental in the problems it treats, and of classic simplicity and power in the results it reaches.
This is a theory so general that one does not need to say what kinds of symbols are being considered - whether written letters or words, or musical notes, or spoken words, or symphonic music, or pictures. The theory is deep enough so that the relationships it reveals indiscriminately apply to all these and to other forms of communication. This means, of course, that the theory is sufficiently imaginatively motivated so that it is dealing with the real inner core of the communication problem - with those basic relationships which hold in general, no matter what special form the actual case may take.
It is an evidence of this generality that the theory contributes importantly to, and in fact is really the basic theory of cryptography which is, of course, a form of coding. In a similar way, the theory contributes to the problem of translation from one language to another, although the complete story here clearly requires consideration of meaning, as well as of information. Similarly, the ideas developed in this work connect so closely with the problem of the logical design of great computers that it is no surprise that Shannon has just written a paper on the design of a computer which would be capable of playing a skillful game of chess. And it is of further direct pertinence to the present contention that this paper closes with the remark that either one must say that such a computer "thinks," or one must substantially modify the conventional implication of the verb "to think."
As a second point, it seems clear that an important contribution has been made to any possible general theory of communication by the formalization on which the present theory is based. It seems at first obvious to diagram a communication system as it is done at the outset of this theory; but this breakdown of the situation must be very deeply sensible and appropriate, as one becomes convinced when he sees how smoothly and generally this viewpoint leads to central issues. It is almost certainly true that a consideration of communication on levels B and C will require additions to the schematic diagram at point 2.1, but it seems equally likely that what is required are minor additions, and no real revision.
Thus when one moves to levels B and C, it may prove to be essential to take account of the statistical characteristics of the destination. One can imagine, as an addition to the diagram, another box labeled "Semantic Receiver" interposed between the engineering receiver (which changes signals to messages) and the destination. This semantic receiver subjects the message to a second decoding, the demand on this one being that it must match the statistical semantic characteristics of the message to the statistical semantic capacities of the totality of receivers, or of that subset of receivers which constitute the audience one wishes to affect.
Similarly one can imagine another box in the diagram which, inserted between the information source and the transmitter, would be labeled "semantic noise," the box previously labeled as simply "noise" now being labeled "engineering noise." From this source is imposed into the signal the perturbations or distortions of meaning which are not intended by the source but which inescapably affect the destination. And the problem of semantic decoding must take this semantic noise into account. It is also possible to think of an adjustment of original message so that the sum of message meaning plus semantic noise is equal to the desired total message meaning at the destination.
Thirdly, it seems highly suggestive for the problem at all levels that error and confusion arise and fidelity decreases, when, no matter how good the coding, one tries to crowd too much over a channel (i.e., H > C). Here again a general theory at all levels will surely have to take into account not only the capacity of the channel but also (even the words are right !) the capacity of the audience. If one tries to overcrowd the capacity of the audience, it is probably true, by direct analogy, that you do not, so to speak, fill the audience up and then waste only the remainder by spilling. More likely, and again by direct analogy, if you overcrowd the capacity of the audience you force a general and inescapable error and confusion.
Fourthly, it is hard to believe that levels B and C do not have much to learn from, and do not have the approach to their problems usefully oriented by, the development in this theory of the entropic ideas in relation to the concept of information.
The concept of information developed in this theory at first seems disappointing and bizarre - disappointing because it has nothing to do with meaning, and bizarre because it deals not with a single message but rather with the statistical character of a whole ensemble of messages, bizarre also because in these statistical terms the two words information and uncertainty find themselves to be partners.
I think, however, that these should be only temporary reactions; and that one should say, at the end, that this analysis has so penetratingly cleared the air that one is now, perhaps for the first time, ready for a real theory of meaning. An engineering communication theory is just like a very proper and discreet girl accepting your telegram. She pays no attention to the meaning, whether it be sad, or joyous, or embarrassing. But she must be prepared to deal with all that come to her desk. This idea that a communication system ought to try to deal with all possible messages, and that the intelligent way to try is to base design on the statistical character of the source, is surely not without significance for communication in general. Language must be designed (or developed) with a view to the totality of things that man may wish to say; but not being able to accomplish everything, it too should do as well as possible as often as possible. That is to say, it too should deal with its task statistically.
The concept of the information to be associated with a source leads directly, as we have seen, to a study of the statistical structure of language; and this study reveals about the English language, as an example, information which seems surely significant to students of every phase of language and communication. The idea of utilizing the powerful body of theory concerning Markoff processes seems particularly promising for semantic studies, since this theory is specifically adapted to handle one of the most significant but difficult aspects of meaning, namely the influence of context. One has the vague feeling that information and meaning may prove to be something like a pair of canonically conjugate variables in quantum theory, they being subject to some joint restriction that condemns a person to the sacrifice of the one as he insists on having much of the other.
Or perhaps meaning may be shown to be analogous to one of the quantities on which the entropy of a thermodynamic ensemble depends. The appearance of entropy in the theory, as was remarked earlier, is surely most interesting and significant. Eddington has already been quoted in this connection, but there is another passage in "The Nature of the Physical World" which seems particularly apt and suggestive:
Suppose that we were asked to arrange the following in two categories - distance, mass, electric force, entropy, beauty, melody. I think there are the strongest grounds for placing entropy alongside beauty and melody, and not with the first three. Entropy is only found when the parts are viewed in association, and it is by viewing or hearing the parts in association that beauty and melody are discerned. All three are features of arrangement. It is a pregnant thought that one of these three associates should be able to figure as a commonplace quantity of science. The reason why this stranger can pass itself off among the aborigines of the physical world is that it is able to speak their language, viz., the language of arithmetic.
I feel sure that Eddington would have been willing to include the word meaning along with beauty and melody; and I suspect he would have been thrilled to see, in this theory, that entropy not only speaks the language of arithmetic; it also speaks the language of language.
Footnotes
(1) "When Pfungst (1911) demonstrated that the horses of Elberfeld, who were showing marvelous linguistic and mathematical ability, were merely reacting to movements of the trainer's head, Mr. Krall (1911), their owner, met the criticism in the most direct manner. He asked the horses whether they could see such small movements and in answer they spelled out an emphatic 'No.' Unfortunately we cannot all be so sure that our questions are understood or obtain such clear answers." See Lashley, K. S., "Persistent Problems in the Evolution of Mind" in Quarterly Review of Biology, v. 24, March, 1949, p. 28.
(2) When mx = y, then x is said to be the logarithm of y to the base m.
(3) The 50 per cent estimate accounts only for statistical structure out to about eight letters, so that the ultimate value is presumably a little higher.
(4) Do not worry about the minus sign. Any probability is a number less than or equal to one, and the logarithms of numbers less than one are themselves negative. Thus the minus sign is necessary in order that H be in fact positive.
(5) We remember that the capacity C involves the idea of information transmitted per second, and is thus measured in bits per second. The entropy H here measures information per symbol, so that the ratio of C to H measures symbols per second.